How and when to use recursion

What is recursion

Taken from wikipedia, recursion is a method of solving a problem where the solution depends on solutions to smaller instances of the same problem. The concept of recursion is actually very mathematical in nature and has a strong basis in recurrence relation. In computer science, recursion happens to work really nicely with functions and is the foundation of several functional languages.

When to use recursion

Like I stated above, recursion is heavily based upon the idea of recurrence relation. Therefore, recursive application in computer science and recurrence relation goes hand in hand.

If you can mathematically model your problem using recurrence relation, you can most definitely write a recursive algorithm to solve your problem.

It also just happens when you derive a recursive problem and each of its sub-problems, you get a really nice tree-looking structure. Therefore, it should be no surprise that a lot of tree-related coding problems are solved using recursion.

How to use recursion

To get started, you need to have the following:

1. Initial condition(s), also known as your base case(s).
2. Recurrence equation

One of the most famous examples is the fibonacci sequence, which can modeled like the following:

Initial conditions

Shorthanding fibonacci to F

F(0) = 0

F(1) = 1

Recurrence equation

F(N) = F(N-1) + F(N-2), where N is an arbitary number.

We can then directly map this into the following code

def fibonacci(n):
  # Initial conditions, F(0), F(1)
  if n == 0: 
   return 0
  if n == 1:
    return 1
  
  # Recurrence equation
  return fibonacci(n-1) + fibonacci(n-2)

How to come up with recurrence equation

To truly solve a recurrence equation, you need to apply mathematical techniques to convert the recursive equations into a closed formula. This can go deep into the realm of discrete mathematics, so I will not talk about it here.

Instead, we can brute force several recursive equations and try to derive the recurrence equation by looking for patterns.

In the case of fibonacci, if we write out the following equations

F(0) = 0

F(1) = 1

F(2) = 1, 1 + 0

F(3) = 2, 1 + 1

F(4) = 3, 1 + 2

F(5) = 5, 2 + 3

We can observe the pattern that the n-th fibonacci number is based on the sum of the previous 2 fibonacci numbers in the same sequence. The only exception being the 0th and the 1st fibonacci number as they do not have previous numbers to build off.

Therefore, the first 2 fibonacci numbers become our initial conditions and the pattern becomes our recurrence equation.

Another example: find all subsequences of a string

Now let's apply the same technique on a real coding problem.

Problem

Given a string, return all subsequences of the string.

"abc" = ["a", "b", "c", "ab", "ac", "abc"]

Recurrence equation

Before doing anything, we need to determine if this problem can be modeled as a recursion problem. To do this, we need to identify its sub-problems.

Since the input is a string, it makes sense to think of the input of the sub problems as substrings of the original input.

Now let us go through several examples to see if we can come up with a recurrence equation.

F("") = []

F(a) = [a]

F(ab) = [a, b, ab], [a] from F(a)

F(abc) = [a, b, c, ab, ac, bc, abc], [a, b, ab] from F(ab)

F(abcd) = [a, b, c, d, ab, ac, ad, bc, bd, cd, abc, abd, bcd, abcd], [a, b,c, ab, ac, bc, abc] from F(abc)

If we observe closely, we can see that the previous output was always contained in the next output, e.g F(abcd) contains F(abc). So we could try to model this as the following:

Initial condition

F("") = []

Recurrence equation

F(N) = F(N-1), N represents the whole string of length N and N-1 represents the substring without the last character,

Solution

class Solution():
  def solve(self, nums):
    arr = []

    self.recursive(nums, "", arr)

    return arr

  # acc is to track and update the string we've build so far.
  def recursive(self, nums, acc, arr):
    n = len(nums)

    # Initial condition, F(0) 
    if len(nums) == 0:
      # Ignore adding "" to our output for the case that we kept choosing to not add.
      if acc != "":
        # Add to our output
        arr.append(acc)
      return

    # Recurrence equation, F(N) = F(N-1)
    self.recursive(nums[:-1], acc, arr) # F(N - 1), ignore last character
    self.recursive(nums[:-1], nums[-1] + acc, arr),  # F(N - 1), add last character

Like I said, a recurrence relation can also be represented in a tree structure. In this problem, we can represent it as a decision tree.

In this tree, each level represents the n-th character and each branch represents the choice to include or exclude the n-th character in our string buildup. The left branch means to exclude and the right branch means to include.

The lowest level are our leaf nodes, which represents our final output.

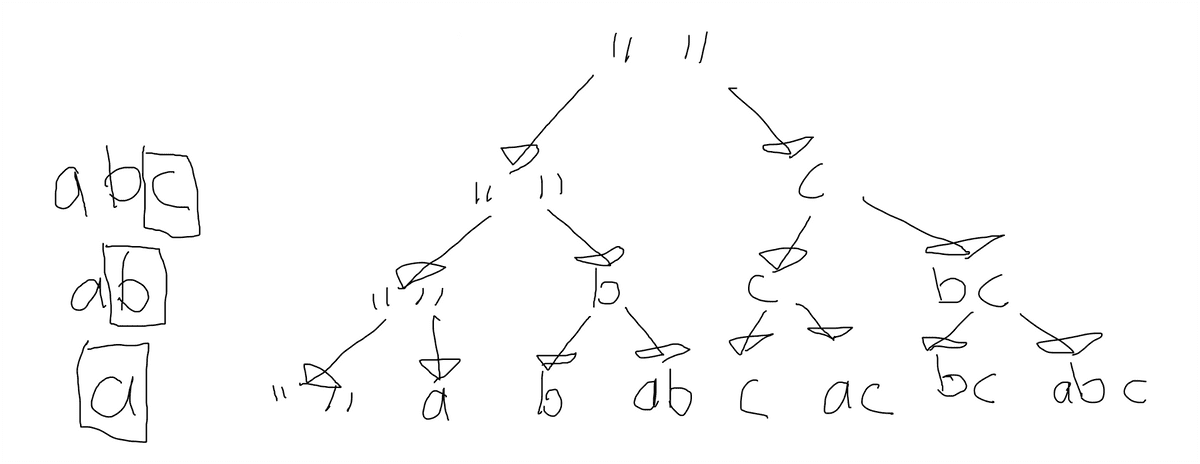
However, this is not the only way to implement the recursion!

As long as you can come up with a valid recurrence equation, you can implement it however you want!

Here's another example using a different recurrence equation!

Different recurrence equation

F(abcd) = []

F(bcd) = [a]

F(cd) = [a, b, ab]

F(d) = [a, b, c, ab, ac, bc, abc]

F("") = [a, b, c, d, ab, ac, ad, bc, bd, cd, abc, abd, bcd, abcd]

F(N) = F(N+1), where N represents the string from the N-th index to its end

This time, our answer actually lies in F("") or F(0)!

class Solution():
  def solve(self, nums):
    arr = []

    self.recursive(nums, 0, "", arr)
    return arr

  def recursive(self, nums, index, acc, arr):
    # Initial condition, F(N) 
    if index >= len(nums):
      if acc != "":
        # Add to our output
        arr.append(acc)
      return

    # Recurrence equation, F(N) = F(N+1)
    self.recursive(nums, index + 1, acc, arr) # F(N + 1), ignore index-th character
    self.recursive(nums, index + 1, acc + nums[index], arr) # F(N + 1), add index-th character

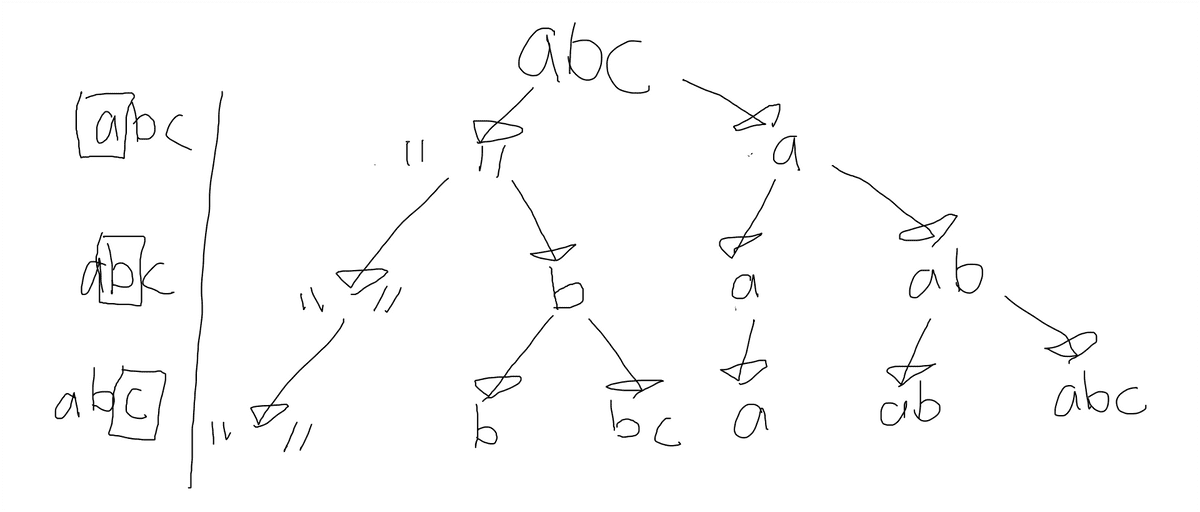
If you're still confused about the two approaches. Here are some explanations in words:

Approach 1

At every recursive call, I remove the last character from the original string and I can either add it or ignore it to my accumulated string

When I've removed all the characters from the original string, I have hit my base case, F(""), I will add my accumulated string.

Approach 2

At every recursive call, I can either ignore or add the current character at this index to my accumulated string. I increment my index for the next recursive call.

When my index exceeds the length of the original string, I have hit my base case, F(abcd) and I will add my accumulated string.